弗洛伊德算法是一种用于寻找带权图中最短路径的算法,应用于具有正右边和负右边(但不能有负环)的图。该算法有时也称为弗洛伊德-沃尔什算法。该算法基于动态规划,时间复杂度为O(V^3),其中V是图中的顶点数。或者,该算法可用于检测方案中的负循环并找到传输闭包。
下面是一个使用弗洛伊德算法来查找图中所有顶点对之间的最短路径的示例:
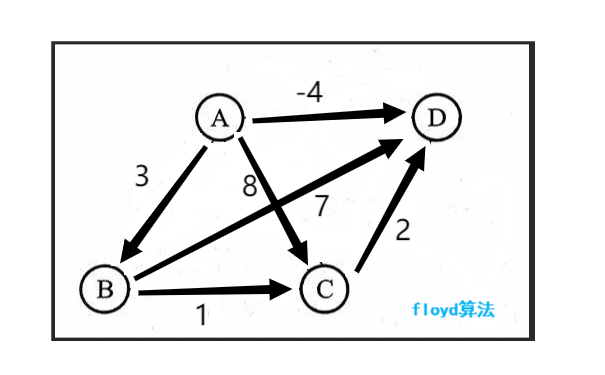
假设我们有一个包含 4 个顶点(A、B、C 和 D)以及以下右边缘的图:
A -> B:3
A -> C:8
A -> D:-4
B -> C:1
乙 -> 丁:7
C -> D:2
我们可以用矩阵来表示每对顶点之间的距离,其中第 i 行 j 列的元素表示顶点 i 到顶点 j 的最短距离。最初,我们将矩阵设置为图中边的值:
| 0 3 8 -4 |
| 信息 0 1 7 |
| 中导 中导 0 2 |
| INF INF 0 |
然后我们使用弗洛伊德算法来更新矩阵:
当 k=1 到 V(V 是顶点数)时,其中 V=4:
对于 i=1 到 V:
当 j=1 到 V 时:
如果 dist[j]>dist[k]+dist[k][j] 则更新 dist[j]=dist[k]+dist[k][j]
当算法运行时,最终矩阵将是:
| 0 3 4 0 | 0 3 4 0
| 信息 0 1 7 |
| 中导 中导 0 2 |
| INF INF 0 |
从这个矩阵,我们可以说,从顶点 A 到顶点 B 的最短距离是 3,从 A 到 C 4,从 A 到 D 0,从 B C 是 1,等等。
本文转载自:https://www.vipshare.com/archives/10955
下面是一个使用弗洛伊德算法来查找图中所有顶点对之间的最短路径的示例:

假设我们有一个包含 4 个顶点(A、B、C 和 D)以及以下右边缘的图:
A -> B:3
A -> C:8
A -> D:-4
B -> C:1
乙 -> 丁:7
C -> D:2
我们可以用矩阵来表示每对顶点之间的距离,其中第 i 行 j 列的元素表示顶点 i 到顶点 j 的最短距离。最初,我们将矩阵设置为图中边的值:
| 0 3 8 -4 |
| 信息 0 1 7 |
| 中导 中导 0 2 |
| INF INF 0 |
然后我们使用弗洛伊德算法来更新矩阵:
当 k=1 到 V(V 是顶点数)时,其中 V=4:
对于 i=1 到 V:
当 j=1 到 V 时:
如果 dist[j]>dist[k]+dist[k][j] 则更新 dist[j]=dist[k]+dist[k][j]
当算法运行时,最终矩阵将是:
| 0 3 4 0 | 0 3 4 0
| 信息 0 1 7 |
| 中导 中导 0 2 |
| INF INF 0 |
从这个矩阵,我们可以说,从顶点 A 到顶点 B 的最短距离是 3,从 A 到 C 4,从 A 到 D 0,从 B C 是 1,等等。
本文转载自:https://www.vipshare.com/archives/10955