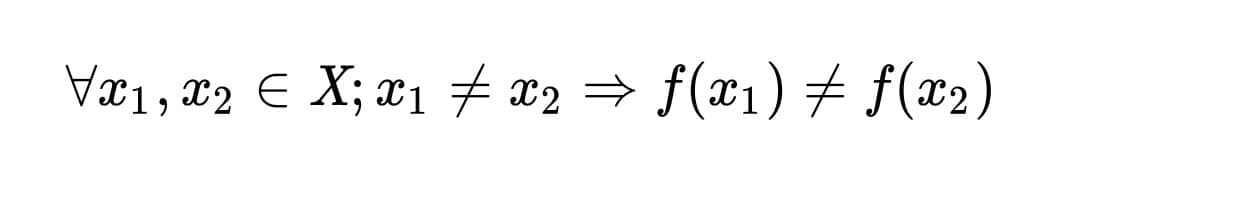Mr.Schrödinger QNVN
Thành viên
- Tham gia
- 2/11/2023
- Bài viết
- 1
Giả thiết continuum hay bài toán continuum là một giả thuyết toán học cho rằng không có tập hợp nào có lực lượng lớn hơn lực lượng của tập các số tự nhiên và nhỏ hơn lực lượng của tập các số thực(dựa trên wikipedia tiếng việt) và ngắn gọn trên wikipedi English là không có tập hợp nào có lực lượng hoàn toàn nằm giữa số nguyên và số thực aka bất kỳ tập hợp con nào của các số thực là hữu hạn, là vô hạn đếm được hoặc có cùng lực lượng với các số thực(Trong lý thuyết tập hợp Zermelo–Fraenkel với tiên đề lựa chọn (ZFC), điều này tương đương với phương trình sau trong aleph number với 2aleph 0=aleph 1) or thậm chí ngắn hơn beth number beth1=aleph1)
----------------------------------------------------------------------------------------------------------------------------
*Góc giải thích về 1 vài khái niệm trên:
-Lực lượng với tiếng việt còn TA có lẽ sẽ gần gũi hơn là cardinality: Lực lượng dùng để chỉ số phàn tử của 1 tập hợp để dễ hiểu ta lấy ví dụ đi
Ta có tập hợp A bao gồm A={1,2,3,4,5}, ở đây t thấy rằng A có 5 phần tử vì vậy lực lượng của A là 5, khái niệm này đc khái quát hóa thành tập hợp vô hạn, cho phép ta phân biệt giữa các loại vô hạn với nhau và cho phép thực hiện phép tính số học trên chúng. Có hai cách tiếp cận đối với lực lượng
+Đầu tiên là: cách so sánh các tập hợp trực tiếp bằng cách sử dụng phép loại và phép tiêm
+Thứ 2 là: sử dụng số lượng lực lượng của tập hợp
Fun fact mà t chắc là đứa nào cx bik: số lượng lực lượng của 1 tập hợp có đc là kích thước của tập hợp ấy
----------------------------------------------------------------------------------------------------------------------------
Tiếp đấy ta đến với việc 2 tập hợp có quan hệ gì với nhau:
Tập hợp X được gọi là có lực lượng nhỏ hơn lực lượng của tập Y nếu ánh xạ từ X vào Y là đơn ánh và không phải là toàn ánh.
Giả thiết này được Georg Cantor nêu ra, sau khi ông chứng minh được lực lượng của hai tập hợp vô hạn là số tự nhiên và số thực là khác nhau, trong đó lực lượng của các số tự nhiên (cardinality countable) nhỏ hơn lực lượng của các số thực (lực lượng continuum).
Giả thiết được thể hiện như sau:
-Aleph0<A<2aleph 0
Với Z tượng trưng cho aleph 0 Là lực lượng của tập hợp vô hạn đếm đc
R tượng trưng cho aleph 0 x aleph 0=aleph 1 là lực lượng của tập hợp vô hạn ko đếm đc
Giả thiết continuum cũng được mở rộng thành giả thiết continuum tổng quát, phát biểu là: nếu S là một tập hợp vô hạn thì không tồn tại tập nào có lực lượng lớn hơn lực lượng của S và nhỏ hơn lực lượng của tập lũy thừa của S. Trường hợp riêng khi S là tập các số tự nhiên, tập lũy thừa của các số tự nhiên có cùng lực lượng với tập số thực, và ta thu được giả thiết continuum ban đầu.
----------------------------------------------------------------------------------------------------------------------------
Góc giải thích về các khái niệm phái trên:
-Ánh xạ: ánh xạ là khái quát của khái niệm hàm số, trong đó tập nguồn và tập đích không nhất thiết phải là tập số thực hay tập con của tập số thực( rõ nhất vẫn là nên
-Hàm số: là một quan hệ hai ngôi giữa hai tập hợp liên kết mọi phần tử của tập hợp đầu tiên với đúng một phần tử của tập hợp thứ hai. Ví dụ điển hình là các hàm từ số nguyên sang số nguyên hoặc từ số thực sang số thực.
-Quan hệ hai ngôi: một quan hệ hai ngôi (hay còn gọi là quan hệ nhị phân) trên hai tập hợp A và B là một tập hợp các cặp được sắp (a, b), chứa các phần tử a thuộc A và các phần tử b thuộc B. Đó là một tập con của tích Descartes A × B. Nó mã hóa thông tin quan hệ: một phần tử a có liên quan với một phần tử b khi và chỉ khi cặp (a, b) thuộc về một tập hợp. Quan hệ hai ngôi là một dạng quan hệ được nghiên cứu nhiều nhất trong số các quan hệ toán học.
-cặp đc sắp: là cặp của hai đối tượng mà thứ tự các đối tượng xuất hiện có ảnh hưởng tới giá trị. Nói cách khác, cặp được sắp (a, b) khác với cặp được sắp (b, a) trừ phi a = b.
-Tích descartes: tích Descartes (hay tích Đềcác) của hai tập hợp A và B, ký hiệu là A×B, là một tập hợp chứa tất cả các bộ có dạng (a, b) với a là một phần tử của A và b là một phần tử của B. Hay, viết trong ngôn ngữ của lý thuyết tập hợp:
+AxB={(a,b)|a thuộc A, b thuộc B}
*Bc ko tìm thấy kí hiệu thuộc nên t ghi ra chữ
Ví dụ, nếu:
A = {1,2}
B = {a,b,c}
Thì khi đó:
A×B = {(1,a),(1,b),(1,c),(2,a),(2,b),(2,c)}
Và
B×A = {(a,1),(b,1),(c,1),(a,2),(b,2),(c,2)}
-Đơn ánh: một hàm số là đơn ánh khi nó áp dụng lên 2 đối số khác nhau luôn cho 2 giá trị khác nhau.
Một cách chặt chẽ, hàm f, xác định trên X và nhận giá trị trong Y, là đơn ánh nếu như nó thỏa mãn điều kiện với mọi x1 và x2 thuộc X và nếu x1 ≠ x2 thì f(x1) ≠ f(x2).
Nghĩa là, hàm số f là một đơn ánh khi và chỉ khi
- Hàm số f của tập hợp X đến tập hợp Y đc gọi là toàn ánh nếu như mọi phần tửu thuộc Y ta luôn tìm đc 1 phần tử của x thuộc X sao cho f(x)=y điều này có nghĩa là mỗi phần tử y của Y đều là ảnh của ít nhất 1 phần tử x thuộc X qua ánh xạ f
----------------------------------------------------------------------------------------------------------------------------
Tiếp đấy ngoài lề tí là về lực lượng của các tập hợp vô hạn:
Hai tập hợp được cho là có cùng lực lượng hoặc số lượng chính nếu tồn tại song ánh (tương ứng một-một) giữa chúng. Theo trực giác, để hai tập hợp S và T có cùng lực lượng nghĩa là có thể "ghép cặp" các phần tử của S với các phần tử của T theo cách sao cho mọi phần tử của S được ghép cặp với đúng một phần tử của T và ngược lại . ngược lại. Do đó, tập hợp {chuối, táo, lê} có cùng lực lượng với {vàng, đỏ, lục}.
Với các tập hợp vô hạn chẳng hạn như tập hợp các số nguyên hoặc các số hữu tỉ , sự tồn tại của phép loại song ánh giữa hai tập hợp trở nên khó chứng minh hơn. Các số hữu tỷ dường như tạo thành một phản ví dụ cho giả thuyết liên tục: các số nguyên tạo thành một tập hợp con thích hợp của các số hữu tỷ, chính chúng tạo thành một tập hợp con thích hợp của các số thực, do đó, theo trực giác, có nhiều số hữu tỷ hơn số nguyên và nhiều số thực hơn số hữu tỷ. Tuy nhiên, phân tích trực quan này là thiếu sót; nó không tính đến thực tế là cả ba tập hợp đều là vô hạn . Hóa ra các số hữu tỉ thực sự có thể được đặt tương ứng 1-1 với các số nguyên, và do đó, tập hợp các số hữu tỉ có cùng kích thước ( cardinality) làm tập hợp các số nguyên: cả hai đều là tập hợp đếm được .
Cantor đã đưa ra hai cách chứng minh rằng số lượng cơ số của tập hợp các số nguyên nhỏ hơn hoàn toàn so với số lượng của tập hợp các số thực. Tuy nhiên, các chứng minh của ông không đưa ra dấu hiệu nào về mức độ mà lực lượng của các số nguyên nhỏ hơn của các số thực. Cantor đề xuất giả thuyết liên tục như một giải pháp khả thi cho câu hỏi này.
Giả thuyết liên tục phát biểu rằng tập hợp các số thực có lực lượng nhỏ nhất có thể lớn hơn lực lượng của tập hợp các số nguyên. Nghĩa là, mọi tập S , các số thực có thể được ánh xạ một đối một vào các số nguyên hoặc các số thực có thể được ánh xạ một đối một vào S . Vì các số thực bằng nhau với lũy thừa của các số nguyên nên |R|=2aleph 0 và giả thuyết liên tục nói rằng không có tập hợp S mà
Aleph 0<|S|<2aleph 0
Giả sử tiên đề của sự lựa chọn tồn tại 1 số hồng y nhỏ nhất duy nhất aleph 1 lớn hơn aleph 0 và giả thuyết liên tục lần lượt tương đương với đẳng thức Aleph zero x Aleph zero=Aleph 1

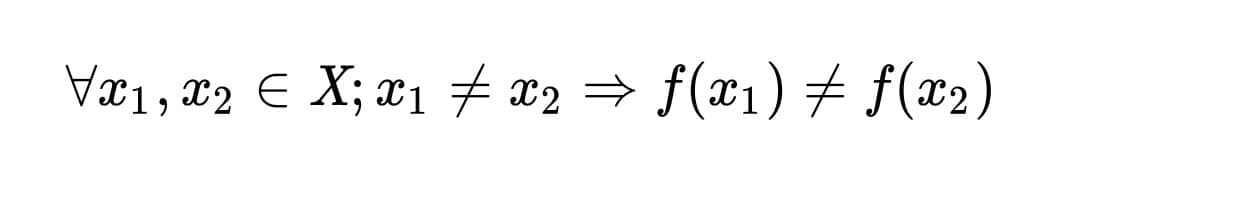
----------------------------------------------------------------------------------------------------------------------------
*Góc giải thích về 1 vài khái niệm trên:
-Lực lượng với tiếng việt còn TA có lẽ sẽ gần gũi hơn là cardinality: Lực lượng dùng để chỉ số phàn tử của 1 tập hợp để dễ hiểu ta lấy ví dụ đi
Ta có tập hợp A bao gồm A={1,2,3,4,5}, ở đây t thấy rằng A có 5 phần tử vì vậy lực lượng của A là 5, khái niệm này đc khái quát hóa thành tập hợp vô hạn, cho phép ta phân biệt giữa các loại vô hạn với nhau và cho phép thực hiện phép tính số học trên chúng. Có hai cách tiếp cận đối với lực lượng
+Đầu tiên là: cách so sánh các tập hợp trực tiếp bằng cách sử dụng phép loại và phép tiêm
+Thứ 2 là: sử dụng số lượng lực lượng của tập hợp
Fun fact mà t chắc là đứa nào cx bik: số lượng lực lượng của 1 tập hợp có đc là kích thước của tập hợp ấy
----------------------------------------------------------------------------------------------------------------------------
Tiếp đấy ta đến với việc 2 tập hợp có quan hệ gì với nhau:
Tập hợp X được gọi là có lực lượng nhỏ hơn lực lượng của tập Y nếu ánh xạ từ X vào Y là đơn ánh và không phải là toàn ánh.
Giả thiết này được Georg Cantor nêu ra, sau khi ông chứng minh được lực lượng của hai tập hợp vô hạn là số tự nhiên và số thực là khác nhau, trong đó lực lượng của các số tự nhiên (cardinality countable) nhỏ hơn lực lượng của các số thực (lực lượng continuum).
Giả thiết được thể hiện như sau:
-Aleph0<A<2aleph 0
Với Z tượng trưng cho aleph 0 Là lực lượng của tập hợp vô hạn đếm đc
R tượng trưng cho aleph 0 x aleph 0=aleph 1 là lực lượng của tập hợp vô hạn ko đếm đc
Giả thiết continuum cũng được mở rộng thành giả thiết continuum tổng quát, phát biểu là: nếu S là một tập hợp vô hạn thì không tồn tại tập nào có lực lượng lớn hơn lực lượng của S và nhỏ hơn lực lượng của tập lũy thừa của S. Trường hợp riêng khi S là tập các số tự nhiên, tập lũy thừa của các số tự nhiên có cùng lực lượng với tập số thực, và ta thu được giả thiết continuum ban đầu.
----------------------------------------------------------------------------------------------------------------------------
Góc giải thích về các khái niệm phái trên:
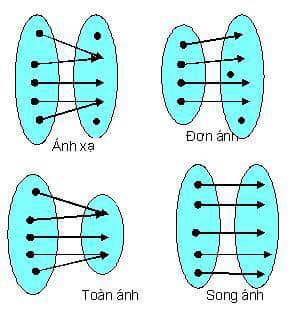
-Ánh xạ: ánh xạ là khái quát của khái niệm hàm số, trong đó tập nguồn và tập đích không nhất thiết phải là tập số thực hay tập con của tập số thực( rõ nhất vẫn là nên
-Hàm số: là một quan hệ hai ngôi giữa hai tập hợp liên kết mọi phần tử của tập hợp đầu tiên với đúng một phần tử của tập hợp thứ hai. Ví dụ điển hình là các hàm từ số nguyên sang số nguyên hoặc từ số thực sang số thực.
-Quan hệ hai ngôi: một quan hệ hai ngôi (hay còn gọi là quan hệ nhị phân) trên hai tập hợp A và B là một tập hợp các cặp được sắp (a, b), chứa các phần tử a thuộc A và các phần tử b thuộc B. Đó là một tập con của tích Descartes A × B. Nó mã hóa thông tin quan hệ: một phần tử a có liên quan với một phần tử b khi và chỉ khi cặp (a, b) thuộc về một tập hợp. Quan hệ hai ngôi là một dạng quan hệ được nghiên cứu nhiều nhất trong số các quan hệ toán học.
-cặp đc sắp: là cặp của hai đối tượng mà thứ tự các đối tượng xuất hiện có ảnh hưởng tới giá trị. Nói cách khác, cặp được sắp (a, b) khác với cặp được sắp (b, a) trừ phi a = b.
-Tích descartes: tích Descartes (hay tích Đềcác) của hai tập hợp A và B, ký hiệu là A×B, là một tập hợp chứa tất cả các bộ có dạng (a, b) với a là một phần tử của A và b là một phần tử của B. Hay, viết trong ngôn ngữ của lý thuyết tập hợp:
+AxB={(a,b)|a thuộc A, b thuộc B}
*Bc ko tìm thấy kí hiệu thuộc nên t ghi ra chữ
Ví dụ, nếu:
A = {1,2}
B = {a,b,c}
Thì khi đó:
A×B = {(1,a),(1,b),(1,c),(2,a),(2,b),(2,c)}
Và
B×A = {(a,1),(b,1),(c,1),(a,2),(b,2),(c,2)}
-Đơn ánh: một hàm số là đơn ánh khi nó áp dụng lên 2 đối số khác nhau luôn cho 2 giá trị khác nhau.
Một cách chặt chẽ, hàm f, xác định trên X và nhận giá trị trong Y, là đơn ánh nếu như nó thỏa mãn điều kiện với mọi x1 và x2 thuộc X và nếu x1 ≠ x2 thì f(x1) ≠ f(x2).
Nghĩa là, hàm số f là một đơn ánh khi và chỉ khi

- Hàm số f của tập hợp X đến tập hợp Y đc gọi là toàn ánh nếu như mọi phần tửu thuộc Y ta luôn tìm đc 1 phần tử của x thuộc X sao cho f(x)=y điều này có nghĩa là mỗi phần tử y của Y đều là ảnh của ít nhất 1 phần tử x thuộc X qua ánh xạ f
----------------------------------------------------------------------------------------------------------------------------
Tiếp đấy ngoài lề tí là về lực lượng của các tập hợp vô hạn:
Hai tập hợp được cho là có cùng lực lượng hoặc số lượng chính nếu tồn tại song ánh (tương ứng một-một) giữa chúng. Theo trực giác, để hai tập hợp S và T có cùng lực lượng nghĩa là có thể "ghép cặp" các phần tử của S với các phần tử của T theo cách sao cho mọi phần tử của S được ghép cặp với đúng một phần tử của T và ngược lại . ngược lại. Do đó, tập hợp {chuối, táo, lê} có cùng lực lượng với {vàng, đỏ, lục}.
Với các tập hợp vô hạn chẳng hạn như tập hợp các số nguyên hoặc các số hữu tỉ , sự tồn tại của phép loại song ánh giữa hai tập hợp trở nên khó chứng minh hơn. Các số hữu tỷ dường như tạo thành một phản ví dụ cho giả thuyết liên tục: các số nguyên tạo thành một tập hợp con thích hợp của các số hữu tỷ, chính chúng tạo thành một tập hợp con thích hợp của các số thực, do đó, theo trực giác, có nhiều số hữu tỷ hơn số nguyên và nhiều số thực hơn số hữu tỷ. Tuy nhiên, phân tích trực quan này là thiếu sót; nó không tính đến thực tế là cả ba tập hợp đều là vô hạn . Hóa ra các số hữu tỉ thực sự có thể được đặt tương ứng 1-1 với các số nguyên, và do đó, tập hợp các số hữu tỉ có cùng kích thước ( cardinality) làm tập hợp các số nguyên: cả hai đều là tập hợp đếm được .
Cantor đã đưa ra hai cách chứng minh rằng số lượng cơ số của tập hợp các số nguyên nhỏ hơn hoàn toàn so với số lượng của tập hợp các số thực. Tuy nhiên, các chứng minh của ông không đưa ra dấu hiệu nào về mức độ mà lực lượng của các số nguyên nhỏ hơn của các số thực. Cantor đề xuất giả thuyết liên tục như một giải pháp khả thi cho câu hỏi này.
Giả thuyết liên tục phát biểu rằng tập hợp các số thực có lực lượng nhỏ nhất có thể lớn hơn lực lượng của tập hợp các số nguyên. Nghĩa là, mọi tập S , các số thực có thể được ánh xạ một đối một vào các số nguyên hoặc các số thực có thể được ánh xạ một đối một vào S . Vì các số thực bằng nhau với lũy thừa của các số nguyên nên |R|=2aleph 0 và giả thuyết liên tục nói rằng không có tập hợp S mà
Aleph 0<|S|<2aleph 0
Giả sử tiên đề của sự lựa chọn tồn tại 1 số hồng y nhỏ nhất duy nhất aleph 1 lớn hơn aleph 0 và giả thuyết liên tục lần lượt tương đương với đẳng thức Aleph zero x Aleph zero=Aleph 1