Nguyễn Thị HuyềnDiệu
Thành viên
- Tham gia
- 24/12/2021
- Bài viết
- 9
ĐỊNH LÍ EUCLID
Định lí Euclid: Qua một điểm ở ngoài một đường thẳng, chỉ có một đường thẳng sonq sonq với đường thẳng đó.(Tiên đề Euclid)
Chứng minh:
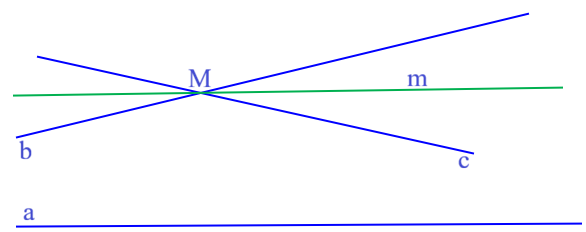
Giả sử qua M có hai đường thẳng b và c cùng song song a.
Vì b//a nên a phải nằm trong một nửa mặt phẳng nào đó có bờ là b. Tương tự vì c//a nên a phải nằm trong một nửa mặt phẳng nào đó có bờ là c. Từ đó a nằm trong phần chung của hai nửa mặt phẳng này, do đó a nằm trong góc do hai đường thẳng b và c cắt nhau tại M tạo ra. Dẫn đến nửa mặt phẳng bờ a không chứa M sẽ nằm trong goc bMc và có npm(a,M) ⊂ ∠bMc.
Gọi số đo góc bMc = α⁰ với 0⁰ < α⁰< 180⁰(*). Ta chia mặt phẳng đã cho thành 360 phần bằng nhau quanh một điểm, mỗi phần là một goc 1⁰.
Ta có: nmp(a,M) ꓴ npm(a,M) = mp(a,M) ⇒ nmp + nnp = mp ⇒ 2nmp = mp ⇒ nmp = (1/2)mp
Như thế nửa mặt phẳng là 1/2 phần của mặt phẳng. Nên diện tích nửa mặt phẳng là 1/2 phần diện tích mặt phẳng.
⇒ Snmp = (1/2)Smp
Và có: mp = ∠(Mc,Mc) = 360⁰ = 360.1⁰ ⇒ Smp = 360. S1⁰
⇒ S1⁰ = (1/360). Smp
Ta cũng có : ∠bMc = α⁰ = α.1⁰ Nên diện tich góc bMc bằng α lần diện tích góc 1⁰.
⇒ S(bMc) = α.S1⁰ = (α/360). Smp
Do npm(a,M) ⊂ ∠bMc ⇒ Snmp < S(bMc) ⇒ (1/2)Smp < (α/360). Smp ⇒ 1/2 < α/360
⇒ α ⩾ 180 ⇒ α⁰ ⩾180⁰ (mâu thuẫn với trên(*).
Vậy qua M chỉ có duy nhât một đường thẳng m sonq sonq với
a mà thôi.□
Chứng minh 2:
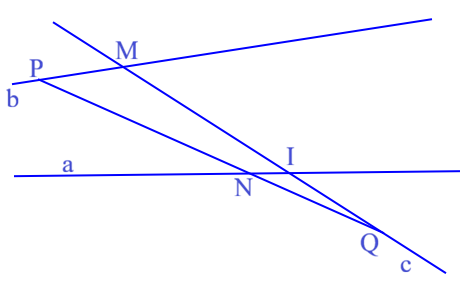
Giả sử qua M có hai đường thẳng b và c cùng song song với a.
Vì b//a nên a phải nằm trong một nửa mặt phẳng nào đó có bờ là b. Tương tự vì c//a nên a phải nằm trong một nửa mặt phẳng nào đó có bờ là c. Từ đó a nằm trong phần chung của hai nửa mặt phẳng này, do đó a nằm trong góc do hai đường thẳng b và c cắt nhau tại M tạo ra và có a ⊂ bMc.
Lấy điểm N ∈ a.Do a ⊂ ∠bMc ⇒ N ⊂ ∠bMc.
Ta có bổ đề sau :
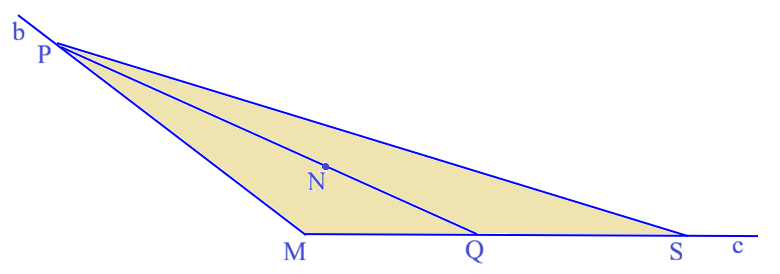
Nếu điểm N nằm trong góc bMc (bMc < 180⁰) thì tồn tại điểm P thuộc Mb, Q thuộc Mc sao cho đoạn thẳng PQ đi qua N.
Thật vậy: Khi điểm N nằm trong góc bMc , lúc đó ăt điểm N phải nằm trên một miền nào đó của goc bMc, do vậy tồn tại P thuộc Mb, và S thuộc Mc, để cho miền tam giac PMS chứa N. Luc này N nằm trong tam giác PMS nên tia PN nằm giữa hai tia PM và PS từ đó tia PN phải cắt MS tại Q, khi đó rõ ràng N nằm giữa P và Q và bổ đề đã được chứng minh.
Đường thẳng a đi qua điểm N nằm giữa P và Q (chú ý đường thẳng PQ ≠ a) nên P và Q sẽ nằm trên hai nửa mặt phẳng đối nhau có chung bờ a.
Do P ∈ b và M ∈ b mà b//a nên M,P cùng thuộc một nửa mặt phẳng bờ a. Suy ra M và Q nằm trên hai nửa mặt phẳng đối nhau có chung bờ a. Nên đường thẳng MQ sẽ cắt a tại một điểm I nào đó.
Mặt khác MQ ≡ c nên ta có c cắt a tại I dẫn đến mâu thuẫn với c//a. Vậy điều giả sử là không đúng. Có nghĩa là qua M không thể có hai đường thẳng b và c cùng song song với a. Hay nói cách khác chỉ có một đường thẳng m đi qua M và sonq sonq với
a mà thôi.□
Định lí Euclid: Qua một điểm ở ngoài một đường thẳng, chỉ có một đường thẳng sonq sonq với đường thẳng đó.(Tiên đề Euclid)
Chứng minh:

Giả sử qua M có hai đường thẳng b và c cùng song song a.
Vì b//a nên a phải nằm trong một nửa mặt phẳng nào đó có bờ là b. Tương tự vì c//a nên a phải nằm trong một nửa mặt phẳng nào đó có bờ là c. Từ đó a nằm trong phần chung của hai nửa mặt phẳng này, do đó a nằm trong góc do hai đường thẳng b và c cắt nhau tại M tạo ra. Dẫn đến nửa mặt phẳng bờ a không chứa M sẽ nằm trong goc bMc và có npm(a,
Gọi số đo góc bMc = α⁰ với 0⁰ < α⁰< 180⁰(*). Ta chia mặt phẳng đã cho thành 360 phần bằng nhau quanh một điểm, mỗi phần là một goc 1⁰.
Ta có: nmp(a,M) ꓴ npm(a,
Như thế nửa mặt phẳng là 1/2 phần của mặt phẳng. Nên diện tích nửa mặt phẳng là 1/2 phần diện tích mặt phẳng.
⇒ Snmp = (1/2)Smp
Và có: mp = ∠(Mc,Mc) = 360⁰ = 360.1⁰ ⇒ Smp = 360. S1⁰
⇒ S1⁰ = (1/360). Smp
Ta cũng có : ∠bMc = α⁰ = α.1⁰ Nên diện tich góc bMc bằng α lần diện tích góc 1⁰.
⇒ S(bMc) = α.S1⁰ = (α/360). Smp
Do npm(a,
⇒ α ⩾ 180 ⇒ α⁰ ⩾180⁰ (mâu thuẫn với trên(*).
Vậy qua M chỉ có duy nhât một đường thẳng m sonq sonq với
a mà thôi.□
Chứng minh 2:

Giả sử qua M có hai đường thẳng b và c cùng song song với a.
Vì b//a nên a phải nằm trong một nửa mặt phẳng nào đó có bờ là b. Tương tự vì c//a nên a phải nằm trong một nửa mặt phẳng nào đó có bờ là c. Từ đó a nằm trong phần chung của hai nửa mặt phẳng này, do đó a nằm trong góc do hai đường thẳng b và c cắt nhau tại M tạo ra và có a ⊂ bMc.
Lấy điểm N ∈ a.Do a ⊂ ∠bMc ⇒ N ⊂ ∠bMc.
Ta có bổ đề sau :

Nếu điểm N nằm trong góc bMc (bMc < 180⁰) thì tồn tại điểm P thuộc Mb, Q thuộc Mc sao cho đoạn thẳng PQ đi qua N.
Thật vậy: Khi điểm N nằm trong góc bMc , lúc đó ăt điểm N phải nằm trên một miền nào đó của goc bMc, do vậy tồn tại P thuộc Mb, và S thuộc Mc, để cho miền tam giac PMS chứa N. Luc này N nằm trong tam giác PMS nên tia PN nằm giữa hai tia PM và PS từ đó tia PN phải cắt MS tại Q, khi đó rõ ràng N nằm giữa P và Q và bổ đề đã được chứng minh.
Đường thẳng a đi qua điểm N nằm giữa P và Q (chú ý đường thẳng PQ ≠ a) nên P và Q sẽ nằm trên hai nửa mặt phẳng đối nhau có chung bờ a.
Do P ∈ b và M ∈ b mà b//a nên M,P cùng thuộc một nửa mặt phẳng bờ a. Suy ra M và Q nằm trên hai nửa mặt phẳng đối nhau có chung bờ a. Nên đường thẳng MQ sẽ cắt a tại một điểm I nào đó.
Mặt khác MQ ≡ c nên ta có c cắt a tại I dẫn đến mâu thuẫn với c//a. Vậy điều giả sử là không đúng. Có nghĩa là qua M không thể có hai đường thẳng b và c cùng song song với a. Hay nói cách khác chỉ có một đường thẳng m đi qua M và sonq sonq với
a mà thôi.□